आइंस्टाइन के द्रव्यमान और ऊर्जा समीकरण का सरल सत्यापन

 

मान लो कि गहन अंतरिक्ष में एक स्थिर डिब्बा तैर रहा है। इस डिब्बे की लंबाई L तथा द्रव्यमान M है। इस डिब्बे से एक E ऊर्जा वाले फोटान का उत्सर्जन होता है और वह बाएं से दायें प्रकाशगति c से जाता है। इस प्रयोग मे सम्पूर्ण प्रणाली के लिये संवेग की अविनाशिता के नियम के पालन हेतु डिब्बे को फोटान के विपरित दिशा मे दायें से बाएं जाना होगा। मान लिजीये की डिब्बे द्वारा तय की गयी दूरी x है, तथा गति v है।

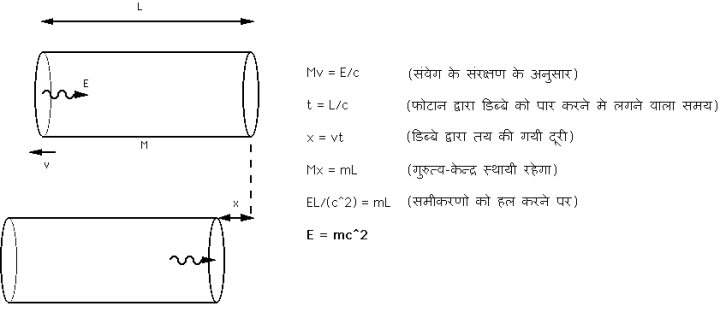
फोटान का संवेग = E/c
डिब्बे का संवेग = Mv

संवेग की अविनाशिता के नियम के अनुसार फोटान का संवेग तथा डिब्बे का संवेग समान होगा।

1) Mv=E/c

फोटान द्वारा डिब्बे को पार करने मे लगने वाला समय

2 ) t=L/c

डिब्बे द्वारा तय की गयी दूरी

3) x=vt

इस समीकरण 3 मे समीकरण 1 और 2 का मूल्य रखने पर

x=[E/(Mc)](L/c)

कुछ समय पश्चात फोटान उसी डिब्बे के दूसरे हिस्से से टकराता है, जिससे उसका संवेग डिब्बे में स्थानांतरित हो जाता है। इस प्रयोग मे पूरे तंत्र का संवेग संरक्षित रहता है, जिससे अब डिब्बे की गति बंद हो जाती है। अब एक समस्या है, इस प्रणाली में कोई बाह्य बल कार्य नहीं कर रहा है, जिससे द्रव्यमान-केंद्र(Center of Gravity) को स्थिर रहना होगा। लेकिन डिब्बे में गति हुयी है। डिब्बे में हुयी गति की पूर्ती द्रव्यमान-केंद्र स्थिर रख कर कैसे होगी? आइन्स्टाइन ने स्पष्ट विरोधाभाष के समाधान के लिए प्रस्तावित किया कि फोटान ऊर्जा का कोई ‘द्रव्यमान समकक्ष‘ होना चाहीये| दूसरे शब्दों में फोटान की ऊर्जा , डिब्बे में द्रव्यमान के बाएं से दायें गति के तुल्य होना चाहिए। साथ में यह द्रव्यमान इतना होना चाहीये कि पूरे तंत्र का द्रव्यमान-केंद्र स्थायी रहेगा।

डिब्बे का द्रव्यमान केन्द्र स्थायी रखने के लिये

4) Mx=mL  (m :फोटान का द्रव्यमान)

समीकरण 4 मे समीकरण 3 द्वारा x का मूल्य रखने पर

5) M [E/(Mc)](L/c)=mL
EL/c2 = mL
E/c2=m
E=mc2